Esta entrada consiste en la solución a la tarea evaluable T3, la cual fue asignada por el profesor Oskar Casquero, cuyo planteamiento se encuentra en el Blog oficial de las asignaturas “Tecnologías de la información y comunicación orientadas a la educación” y “Recursos y herramientas asíncronas para el trabajo colaborativo educativo” y se puede acceder en el siguiente enlace: Tarea evaluable T3.
Respuesta
1.- Observar los datos y reflexionar acerca de la relación que existe entre las variables calificación, grupo y sexo.
Para esta parte de la asignación, abrí el fichero que contiene los datos de esta asignación en el programa de Hojas de cálculo de Google. Viendo los datos pude notar que las calificaciones de los estudiantes que utilizaban la plataforma de Moodle eran inferiores a los que estudiaban la plataforma Google Apps. En cuanto a las calificaciones atendiendo al sexo, no me fue posible llegar a una conclusión con respecto a cuales eran mayores analizándolas a simple vista.
2.- Dibujar en Excel o Google Sheets un gráfico de interacción (http://courses.washington.edu/smartpsy/interactions.htm) de las medias de las calificaciones combinando las variables grupo y sexo, es decir: Moodle-Male, Moodle-Female, GoogleApps-Male, GoogleApps-Female. ¿Coinciden los resultados mostrados en el gráfico con tus reflexiones del apartado anterior?
Para esta parte de la asignación, utilicé nuevamente el programa Hojas de Cálculo de Google. Obtuve las medias de las diferentes combinaciones, Moodle - Male, Moodle - Female, Google Apps - Male y Google Apps - Female, esto lo hice mediante la función PROMEDIO.SI.CONJUNTO (AVERAGEIFS) del programa usado, la cual sirve para obtener la media de un rango de celdas, siempre y cuando cumplan con las condiciones dadas, en este caso, que pertenezcan al grupo y al sexo requerido.
De esa forma obtuve las siguientes medias: Moodle - Male = 4.6, Moodle - Female = 5.9, Google Apps - Male = 7.9 y Google Apps - Female = 6.6.
Utilizando esas medias, hice el siguiente gráfico de interacción:
Video para hacer el mismo proceso en Excel
Observando dicho gráfico, pude percibir que efectivamente, la media de los estudiantes que utilizan Google Apps, tanto masculino como femenino, es superior a los que utilizan Moodle, lo cual está en consonancia con lo que pude determinar en el paso anterior.
Observando dicho gráfico, pude percibir que efectivamente, la media de los estudiantes que utilizan Google Apps, tanto masculino como femenino, es superior a los que utilizan Moodle, lo cual está en consonancia con lo que pude determinar en el paso anterior.
En lo que se refiere a las notas tomando en consideración el sexo del estudiante, se puede observar que ninguno de los dos presenta representa los valores más altos, ya que los estudiantes masculino obtuvieron tanto la media más baja (Moodle - Masculino) como la media más alta (Google Apps - Masculino).
En cuanto a lo que se refiere a si hay o no interacción, según lo consultado en el material ofrecido por el profesor, se puede determinar que sí; puesto que el efecto de una de las variables independientes depende del nivel de la otra variable independiente. Si observamos en el gráfico, el cambio de plataforma de Moodle a Google Apps si bien aumenta tanto para el caso femenino como para el masculino, está influenciado por el sexo, ya que en un caso aumenta una cantidad considerable y en otro en menor proporción. Se observa que la variable grupo tiene un efecto principal, mientras que la variable sexo no tiene un efecto principal.
Conviene señalar que si bien el gráfico sugiere la existencia de interacción, es necesario analizar si dicha interacción se debe a la casualidad, lo cual se hace más adelante.
3.- Analizar si existen diferencias estadísticamente significativas en las calificaciones en función del grupo y del sexo.
Conviene señalar que si bien el gráfico sugiere la existencia de interacción, es necesario analizar si dicha interacción se debe a la casualidad, lo cual se hace más adelante.
3.- Analizar si existen diferencias estadísticamente significativas en las calificaciones en función del grupo y del sexo.
Paso 1: Abrí el fichero en RStudio, de la misma manera como lo hice en la Tarea Evaluable T2:
Paso 2: Procedí a dividir los datos en función del grupo y del sexo.
a) Datos en Moddle
datos3Moodle <- subset(datos3, grupo=="Moodle")
b) Datos en Google Apps
datos3GoogleApps <- subset(datos3, grupo=="Google Apps")
c) Datos Masculino
datos3Masculino <- subset(datos3, sexo=="M")
d) Datos Femenino
datos3Femenino <- subset(datos3, sexo=="F")
Paso 3: Luego comparé los datos para ver si existían diferencias significativas por grupo y por sexo.
a) Comparación por grupo:
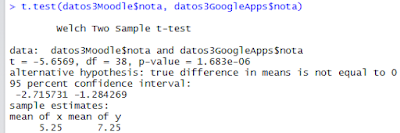
t.test(datos3Moodle$nota, datos3GoogleApps$nota)
El análisis de los resultados demuestra que hay diferencias estadísticamente significativas, entre los dos grupos de estudiantes. Porque el margen de error es menor de un cinco por ciento, en virtud de que p-value = 1.683e-06, es decir 0.000001683, lo que equivale a un 0.0001683%, que es la probabilidad de obtener resultados diferentes haciendo el mismo estudio, utilizando una muestra semejante.
b) Comparación por sexo:
t.test(datos3Masculino$nota, datos3Femenino$nota)
El análisis de los resultados muestra que por sexo no hubieron diferencias estadísticamente significativas entre los estudiantes. Porque el margen de error es mayor que un cinco por ciento, en virtud de que p-value =1, lo que equivale a un 100%.
4.- Utilizar la función aov() de R para saber si existe una interacción estadísticamente significativa entre las variables grupo y sexo.
Para aprender sobre el uso de la función aov() en R, consulté los siguientes aportes: http://courses.statistics.com/software/R/Rtwoway.htm y http://www.stat.columbia.edu/~martin/W2024/R8.pdf, ya que no había tenido ninguna experiencia con dicha función.
Utilicé la función aov(), en el interior de la sentencia summary(), para analizar la interacción entre las variables grupo y sexo. Para ello la función aov() necesita que le sea pasado por argumento en primer lugar la variable dependiente, seguida del símbolo “~” y posteriormente las dos variables independientes separadas por un “*”.
summary(aov(datos3$nota ~ datos3$grupo*datos3$sexo))
El análisis de los resultados indica que hay una interacción estadísticamente significativa entre las variables grupo y sexo, puesto que el valor de p para la interacción es de 7.74e-05, lo que equivale a 0.0000774, lo que es igual a un 0.00774%, que es mucho menor al margen de error de 5%.
Reflexión Personal
Para completar la presente asignación me fue necesaria la investigación. Primero investigué acerca de la interacción, tanto en el material presentado por el profesor como en otros recursos en línea. Posteriormente me investigué sobre el uso de la función aov(), lo cual hice también en varias fuentes.
En tal sentido adquirí conocimientos en el área de la estadística, con conceptos como la interacción, efecto principal y análisis de varianza. También pude adquirir nuevos conocimientos acerca de R, como el uso de la función attach() y otras más, que si bien no utilicé en este aporte, me servirán para el aporte sobre R que subiré más adelante.





0 comentarios:
Publicar un comentario